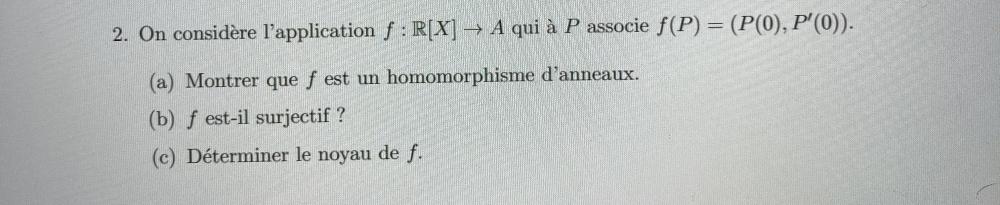Chaka

Je viens de finir mon script cependant je rencontre un problème par rapport aux résultats que j'obtiens : cf pièces jointes et scripts. La première est la figure que j'obtiens avec RK4 (convergence vers l'origine), la seconde avec la méthode de Newton (aspect chaotique). (avec les mêmes constantes et les mêmes conditions initiales) Trouvez-vous une explication à ces différences ? Si non, problèmes dans les scripts ? : ## Euler NS-Lorenz def lorenz(x, y, z, s=10, r=28, b=2.667): """ Entrée: x, y, z: point dans R3 auquel nous nous interessons s, r, b: paramètres de l'attracteur de Lorenz Sortie: dérivées partiels aux points x, y, z liées aux équations de Lorenz """ x_dot = s*(y - x) y_dot = r*x - y - x*z z_dot = x*y - b*z return x_dot, y_dot, z_dot pas = 0.01 num_iter = 10000 # +1 pour prendre les CI x_sol = np.empty(num_iter + 1) y_sol = np.empty(num_iter + 1) z_sol = np.empty(num_iter + 1) # CI : Conditions initiales x_sol[0], y_sol[0], z_sol[0] = (0., 1., 1.05) # Euler for i in range(num_iter): x_dot, y_dot, z_dot = lorenz(x_sol[i], y_sol[i], z_sol[i]) x_sol[i + 1] = x_sol[i] + (x_dot * pas) y_sol[i + 1] = y_sol[i] + (y_dot * pas) z_sol[i + 1] = z_sol[i] + (z_dot * pas) # Plot ax = plt.figure().add_subplot(projection='3d') ax.plot(x_sol, y_sol, z_sol, lw=0.5) ax.set_xlabel("X") ax.set_ylabel("Y") ax.set_zlabel("Z") ax.set_title("Attracteur de Lorenz") plt.show() ## RK4 NS-Lorenz s,r,b=10,28,2.667 #Lorenz def f(t,x,y,z): return s*(y-x) def g(t,x,y,z): return r*x-y-x*z def h(t,x,y,z): return x*y-b*z # Initialisation x,y,z=[0],[1],[1.05] pas=0.01 num_iter=10000 #t=pas*num_iter t=np.linspace(0,pas*num_iter,num_iter+1) # RK4 for i in range (num_iter): k1=pas*f(t[i],x[i],y[i],z[i]) l1=pas*g(t[i],x[i],y[i],z[i]) m1=pas*f(t[i],x[i],y[i],z[i]) k2=f(t[i]+pas/2,(x[i]+k1*pas/2),(y[i]+(l1*pas/2)),(z[i]+(m1*pas/2))) l2=g(t[i]+pas/2,(x[i]+k1*pas/2),(y[i]+(l1*pas/2)),(z[i]+(m1*pas/2))) m2=h(t[i]+pas/2,(x[i]+k1*pas/2),(y[i]+(l1*pas/2)),(z[i]+(m1*pas/2))) k3=f(t[i]+pas/2,(x[i]+k1*pas/2),(y[i]+(l1*pas/2)),(z[i]+(m1*pas/2))) l3=g(t[i]+pas/2,(x[i]+k1*pas/2),(y[i]+(l1*pas/2)),(z[i]+(m1*pas/2))) m3=h(t[i]+pas/2,(x[i]+k1*pas/2),(y[i]+(l1*pas/2)),(z[i]+(m1*pas/2))) k4=f(t[i]+pas,(x[i]+k3*pas),(y[i]+l3*pas),(z[i]+m3*pas)) l4=g(t[i]+pas,(x[i]+k3*pas),(y[i]+l3*pas),(z[i]+m3*pas)) m4=h(t[i]+pas,(x[i]+k3*pas),(y[i]+l3*pas),(z[i]+m3*pas)) x.append(x[i]+pas*(k1+2*k2+2*k3+k4)/6) y.append(y[i]+pas*(l1+2*l2+2*l3+l4)/6) z.append(z[i]+pas*(k1+2*k2+2*k3+k4)/6) # Plot ax = plt.figure().add_subplot(projection='3d') ax.plot(x, y, z, lw=0.5) ax.set_xlabel("X") ax.set_ylabel("Y") ax.set_zlabel("Z") ax.set_title("Attracteur de Lorenz") plt.show()

Merci beaucoup julesx !! Je viens de lire le dernier post de ce forum et cela à l'air de répondre à ma question. Entre temps j'avais un peu avancé et étais en bonne voie d'après ce que je viens de lire. Je t'en remercie ! Je posterai le code final pour ceux que cela intéresse Bonne soirée

Je confirme que ce que tu as dit est mal rédigé. Grand bien te fasse de rester borné. Bref je ne veux pas tomber dans un débat stérile avec toi car il ne nous apporterai rien à tout les deux si ce n'est que des ennuis. Bien cordialement. Bonne continuation

Lorenz avec la méthode d'Euler : def lorenz(x, y, z, s=10, r=28, b=2.667): """ Entrée: x, y, z: point dans R3 auquel nous nous interessons s, r, b: paramètres de l'attracteur de Lorenz Sortie: dérivées partiels aux points x, y, z liées aux équations de Lorenz """ x_dot = s*(y - x) y_dot = r*x - y - x*z z_dot = x*y - b*z return x_dot, y_dot, z_dot pas = 0.01 num_iter = 10000 # +1 pour prendre les CI x_sol = np.empty(num_iter + 1) y_sol = np.empty(num_iter + 1) z_sol = np.empty(num_iter + 1) # CI : Conditions initiales x_sol[0], y_sol[0], z_sol[0] = (0., 1., 1.05) # Euler for i in range(num_iter): x_dot, y_dot, z_dot = lorenz(x_sol[i], y_sol[i], z_sol[i]) x_sol[i + 1] = x_sol[i] + (x_dot * pas) y_sol[i + 1] = y_sol[i] + (y_dot * pas) z_sol[i + 1] = z_sol[i] + (z_dot * pas) # Plot ax = plt.figure().add_subplot(projection='3d') ax.plot(x_sol, y_sol, z_sol, lw=0.5) ax.set_xlabel("X") ax.set_ylabel("Y") ax.set_zlabel("Z") ax.set_title("Attracteur de Lorenz") plt.show() Runge Kutta d'odre 4 : def rk4(f,t0,tf,y0,N): y=[y0] t=np.linspace(t0,tf,N+1) pas=(tf-t0)/N #Initialisation k1=[f(y[i],t[i])] k2=[y0+(pas/2)*f(t0,y0)] k3=[y0+(pas/2)*f(t0+pas/2,k1[0])] k4=[y0+pas*f(t0+(pas/2),k2[0])] for i in range(N): y.append(y[i]+(pas/6)*(f(t[i],y[i])+2*f(t[i]+pas/2,k2[i])+2*f(t[i]+(pas/2),k3[i-1])+f(t[i+1],k4[i]))) k2.append(y[i+1]+(pas/2)*f(t[i+1],y[i+1])) k3.append(y[i+1]+(pas/2)*f(t[i+1]+(pas/2),k2[i+1])) return t,y

Bonsoir. Je te parlais du message que j'ai précédemment cité : "[...] Poser t^(n-1) = u --> (n-1).t^(n-2) dt = du et poser t * exp((-t^2)/25) dt = dv ---> v = -(25/2) *exp((-t^2)/25) [...] u = t^(n-1) et v' = t * exp((-t^2)/25)". Ce qui est écrit ici c'est un changement de variable. Ici tu as juste posé une variable u= une expression en fonction de t et non u_n(t)= une expression de t (qui serait donc bien une fonction de t). Sur ce ... Bonne soirée

Je vais reposter mon script de la partie qui m'intéresse dans ce cas . Merci

Bonjour, Dans le cadre d'un projet d'étude (3ème année de Licence), je voudrais mettre en place, sur Python, la méthode de RK4 pour résoudre les équations de Lorentz numériquement. J'ai réussi à le faire sans trop de difficulté avec les méthodes de Newton, mais pour RK4, je bloque !! Le calcul des intermédiaires m'est compliqué. Je vous mets ci-joint mes scripts Python. Merci par avance pour vos retours. Chaka PS: ce post à déjà été émis dans le forum Mathématiques. Projet P.py

Il m'est compliqué notamment car ma fonction lorenz est de R^3 dans R^3 mais chaque composante nécessite les autres pour son calcul et ma fonction RK4 prend des valeurs dans R si je ne dis pas d'idioties.

Et ceci s'appelle un changement de variable !! Pzorba n'est donc pas fou...

Bonjour, Dans le cadre d'un projet d'étude (3ème année de Licence), je voudrais mettre en place, sur Python, la méthode de RK4 pour résoudre les équations de Lorentz numériquement. J'ai réussi à le faire sans trop de difficulté avec les méthodes de Newton, mais pour RK4, je bloque !! Le calcul des intermédiaires m'est compliqué. Je vous mets ci-joint mes scripts Python. Merci par avance pour vos retours. Chaka Projet P.py

Bon... j'ai passé plus de 1h à trouver ma bêtise mais finalement j'y suis arrivé... !!!! Je vous note la coquille que j'ai faite : renewcommand{\thechapter}{\Roman{chapter})} \renewcommand{\thesection}{\Roman{section})} \renewcommand{\thesubsection}{\alph{subsection})} \renewcommand{\thesubsubsection}{\roman{subsubsection}}

Bonjour/Bonsoir, Je me permets de vous contacter car je rencontre un problème dans mon script LaTeX : numérotation des sous-sous-sections. Je réussis à les numéroter mais elles se numérotent toutes comme étant au deuxième rang... Etrange !! Si quelqu'un a la solution ... ! Merci par avance ! Chaka Script ci-joint : \documentclass[french]{report} \usepackage{babel} \usepackage[T1]{fontenc} \usepackage{geometry} \usepackage{amsmath} \usepackage{hyperref} \usepackage{amssymb} \usepackage{amsfonts} \usepackage{dsfont} \usepackage{listings} \usepackage{fancybox} \usepackage{epsfig} \usepackage[dvipsnames]{xcolor} \usepackage[utf8]{inputenc} \usepackage{libertine} \usepackage[pdftex]{graphicx} \setcounter{secnumdepth}{3} \setcounter{tocdepth}{3} \renewcommand{\thechapter}{\Roman{chapter})} \renewcommand{\thesection}{\Roman{section})} \renewcommand{\thesubsection}{\alph{subsection})} \renewcommand{\thesubsubsection}{\roman{section}} \setlength{\parindent}{0cm} \setlength{\parskip}{1ex plus 0.5ex minus 0.2ex} \newcommand{\hsp}{\hspace{20pt}} \newcommand{\HRule}{\rule{\linewidth}{0.5mm}} \begin{document} \begin{titlepage} \begin{sffamily} \begin{center} \textsc{\LARGE Faculté des sciences et techniques de Limoges}\\[2cm] \textsc{\Large Projet Sytèmes différentiels Licence 3}\\[1.5cm] \HRule \\[0.4cm] { \huge \bfseries Les intégrales de Wallis\\[0.4cm] } % Bottom of the page \HRule \\[1cm] {\large Dossier réalisé par DELAUNAY Evan et GLUKHOVA Marina} \\[2cm] \includegraphics[scale=0.8]{logo.png} \\[4cm] {\large Dossier à rendre pour le 10 mai 2021} \end{center} \end{sffamily} \end{titlepage} \tableofcontents \begin{flushleft} \newpage \section{Introduction} blablabla \newpage \section{Algorithmes de résolution de systèmes différentiels} \subsection{Préambule} \subsubsection{1} \subsubsection{2} \subsubsection{3} \subsubsection{4} \newpage \subsubsection{Méthodes de Runge Kuta} développement + code \begin{lstlisting} import numpy as np \end{lstlisting} \newpage \section{Attracteur de Lorenz} \subsection{Préambule} \subsection{Application} \subsection{Interprétations} \end{flushleft} \end{document}

Bonjour à tous. Je tente de démontrer cette proposition (cf pièce-jointe). Je bloque sur la demo du premier point et ai réussi le second. Si quelqu'un a une piste ... je suis preneur. Bonne journée Proposition page 43_210126_120106.pdf

Finalement j'ai eu ma réponse (par moi même). Je vous poste le corrigé ci-dessous. TD 1 ~ OCA_210122_155208.pdf

Bonjour a tous, Besoin d'une confirmation sur un énoncé ! En effet je pense qu'il y a une coquille dedans. Je vous laisse regarder la pièce jointe et réagir. Si l'énoncé est bon alors je ne vois pas comment faire ! Merci par avance pour vos retours.

Bonjour, Il y a l'air d'avoir un soucis en effet! L'égalité n'a pas lieu d'être. Bonne journée

Voici la suite (page 3) Bonne soirée Et surtout, n'hésite pas à poser des questions !! Sans_titre (1).pdf

Bonjour, En pièce-jointe, le premier exo. N'hésite pas à poser des questions ! Je fais le deuxième et le poste dans quelques minutes Sans_titre.pdf

Bonjour à tous, Je me permets de poster ce petit exercice ici. Pour montrer qu'il s'agit d'un homomorphisme d'anneaux, je dois montrer ces points suivants: Je montre trivialement que f(1R[X])=1A et que f(P1+P2)=f(P1)+f(P2) Cependant, je bloque sur le point f(P1*P2)=f(P1)*f(P2) Si quelqu'un peut m'aider dans le développement notamment sur le polynôme dérivé (dérivée d'un produit de polynome donc j'utilise leibniz et j'ai donc P1'P2 + P1P2' ) Merci par avance pour vos retours. Chaka

Bonsoir, Gros doute sur cette question (cf pièce-jointe). Dois-je juste redémontrer les racines nième de l'unité ? On aurait donc bien le nombre de 0 des Fn qui serait fini. J'ai pensé résoudre z^n -1=0 et donc les solutions sont S = { exp(i 2k pi / n), k € [|0,n-1|] } (désolé pour l'écriture moche) Je ne sais pas si c'est cohérent ... Je mets également en pièce jointe le sujet complet du TP. Merci par avance pour vos retours ! Chaka an1_tp2.pdf

Bonsoir ! Actuellement en L3 Maths en ayant fait auparavant une prépa MPSI-MP, je pense pouvoir te donner mon opinion ! Au vu de ce que tu as dit, tu as le niveau et la mentalité pour aller en prépa en maths, cependant tu n'as pas la physique ce qui risque de te fermer des portes. Cependant, tu peux toujours essayer d'intégrer une prépa pour ensuite tenter l'ENS, un magistère ou bien juste reprendre la fac. De ce que j'ai vu, en sortant de prépa, les élèves de fac arrivant en L3 sont bien moins bons que les élèves arrivant de prépa. Pour avoir discuter avec des ex-L1 et ex-L2 de Maths, le programme de L1 en lui même n'est pas très dur, ils introduisent beaucoup de notions très générales (que tu approfondiras en L3 et qui te suivront peu importe la filière scientifique) exemple "le langage mathématique". La différence avec la prépa se fait au niveau de la rigueur et de l'intensité des cours. Je ne peux pas te dire si le programme "général" du lycée en physique est adapté à la L1 "pluridisciplinaire" car j'étais en Term S donc même programme pour tous. En espérant t'avoir éclairer sans trop avoir parler des CPGE En résumé, je pense que la fac en L1 est accessible pour peu que tu ais un peu fait de physique en parallèle de ta spé Maths (pour l'informatique, cela va avec les maths). Bon courage à toi ! Je reste à ta disposition si tu as des questions. Chaka