PAVE

Exercice 3 : Si tu avais regardé la COURBE de f, tu aurais su que ta réponse était fausse....

Exercice 1 : il te faut COMPLETER le tableau de variation de f on y faisant figurer les valeurs particulières (maximum et minimum) et aussi les limites à l'infini.

Bonsoir, Pour l'autre exercice, il te faut exploiter les informations données par l'énoncé. A savoir : f(1) = 1/2 Propriété 01 (P01) et surtout cette "bizarrerie" que : f(x+y) = f(x)*f(y) Propriété 02 (P02) [NB : le signe * est celui de la MULTIPLICATION]. 1) Il te faut trouver la valeur de f(2) . Si on écrit 2 sous forme d'une somme x+y : 2= 1+1, alors d'après P02 puis P01, f(2) =.... on aboutit à f(2) = ?? 2) Reste à déterminer f(0). Même procédé ou presque : tu peux écrire que 0+1 = 1. Applique la propriété P02 puis P01.... Je te laisse finir. Pense à calculer la somme finale.

Si tu relis attentivement l'énoncé, la fonction h est involutive si hoh(x)=x Le calcul de hoh(x) qui en découle est un peu délicat mais il se simplifie très vite... et n'oublie pas que tu CONNAIS le résultat à obtenir 😉.

As tu fait l'exercice 3 ? f est de la forme eu donc f ' est de la forme.... Cela c'est du cours que tu dois savoir. L'étude de la fonction f ne pose pas de problème ; c'est de l'ultra classique 1) domaine de déf ? avec une exponentielle... 2) calcul de la fonction dérivée 3) étude du signe de la dérivée puis tableau de variation de f 4) penser à vérifier en jetant un œil sur la courbe de f Essaye et montre ce que tu obtiens ; on te dira si c'est bon mais surtout, s'il y a un problème dans tes réponses, on te dira comment faire...pour ne plus refaire cette erreur 🤥

Par contre tu as dû voir en cours la notion de fonction composée....et cela suffit pour traiter cet exercice 🙂 !! Dans mon message, je t'ai rappelé la définition de h= gof (cela tu dois connaitre) et en application j'ai proposé le cas particulier où g est égal à f => h=fof soit h(x) = f[f(x)] Prends la fonction f donnée dans ton exercice et calcule f[f(x)]. Essaye....

Quelques rappels :

Cela me fait plaisir de te voir réapparaitre sur ce fil. C'est bien de persévérer. On va t'aider d'autant plus que les réponses que tu as données sont bonnes comme te l'a dit Jules (merci à lui d'avoir pris le relai... et bonne année à vous deux☺️). Dans l'étude d'une fonction f, 1. on calcule la fonction dérivée f ' . Tu as obtenu ici f '(x) = 3x²+6x-45 qui est un polynôme du second degré (si besoin revoir le cours de 1ère 😟) 2. on étudie le SIGNE de f '(x) la dérivée : en première tu as appris à étudier le SIGNE d'un trinôme du second degré ax²+bx+c (à revoir si besoin) On présente le résultat sous forme d'un tableau.... donnant le SIGNE de la dérivée. valeurs de x |.................. Signe de f '(x)|......................... 3. le SIGNE de la dérivée f ' donne le SENS DE VARIATION de la fonction f. On présente le résultat sous forme d'un tableau de VARIATION. On peut simplement ajouter une ligne au tableau de Signes précédent. valeurs de x |.................. Signe de f '(x)|......................... SENS de variation de f | 4. on vérifie que le tableau obtenu est cohérent (compatible) avec la courbe représentative de f (avec un peu d'expérience, 2 minutes suffisent pour obtenir cette courbe sur ta calculatrice... VERIFIER est fondamental !!)

Bonjour, Il y a bien longtemps que je n'avais trouvé cette notion (l'involution) dans un exercice de lycée. ll serait intéressant de savoir comment cette notion est abordée en Terminale.

suite Pour t'encourager un peu : a) RElire attentivement l'énoncé b) est-ce que tu connais ce "type" de fonction ? oui, c'est une fonction POLYNOME (ici de degré 3, puisque le monôme (de la forme axn ) de plus haut degré est x³.... la puissance de x est 3. c) comment "dérive-t-on un polynôme" ? on dérive successivement chaque terme (= monôme) x³ a pour dérivée ? 3x² à pour dérivée ? etc....

Si tu as besoin d'un peu d'AIDE, nous pouvons t'en donner BEAUCOUP 🙂... Principe : 1) tu poses une question ; on te réponds et on te demande de faire quelque chose (un calcul, une recherche...) 2) tu réponds du mieux que tu peux à notre demande ; on commente ta réponse et si besoin on te propose une nouvelle action (calcul, recherche 3) etc . jusqu'à ce que TU obtiennes la solution de ton problème. C'est un tchat qui peut avancer très vite si tu réponds très vite.... Nous on est là en continu. Application : Pour l'exercice 1, il faut déterminer la fonction dérivée de la fonction f. Tu as essayé ? qu'as tu trouvé (même si tu penses que c'est faux , dis ce que tu as obtenu et éventuellement comment tu l'as obtenu). A toi de répondre... j'attends ta participation 🤔.

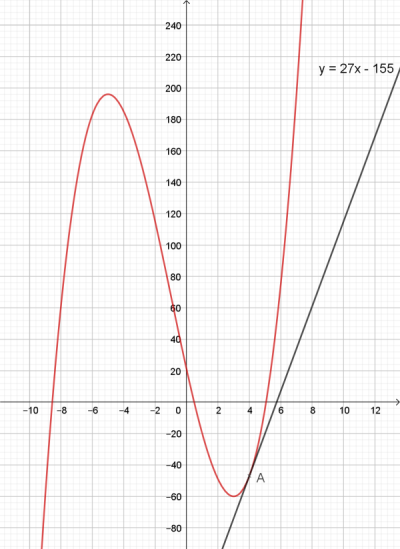
suite En guise d'étrenne ☺️, voici un petit cadeau qui pourra t'aider à VERIFIER TES REPONSES (tu peux obtenir la courbe représentative de f avec ta super calculatrice)

Bonsoir, Bienvenue sur ce site de soutien scolaire gratuit. Nous sommes à ta disposition pour t'AIDER à traiter ces exercices. Mais si ce que tu attends de nous est que nous fassions le travail à ta place je crains que tu ne te sois trompé d'adresse. Regarde le premier exercice, il est tout a fait CLASSIQUE : regarde (et apprends) ton cours, revois les exercices faits en classe et... mets toi au travail. Il n'y a aucune difficulté... Essaie de trouver la dérivée de f(x) et montres nous ce que tu trouves. Si ta réponse est fausse alors on essaiera ENSEMBLE de comprendre pourquoi ton calcul est faux. Puis on te conduira jusqu'à la solution. A toi de voir si notre méthode d'AIDE peut te convenir 🙂. PS : à l'avenir, évite de mettre 4 exercices dans un même message.

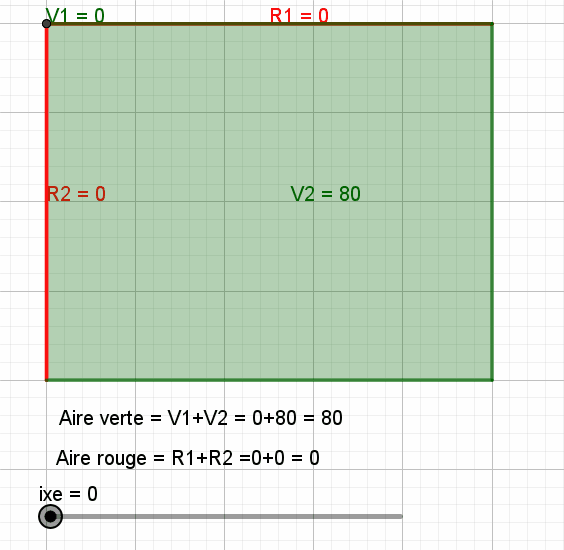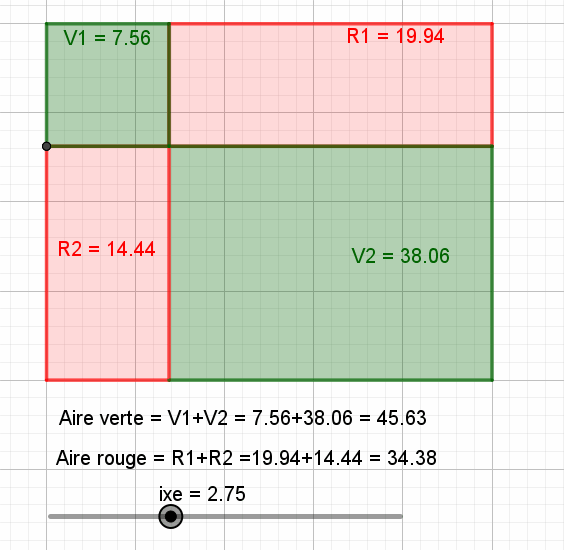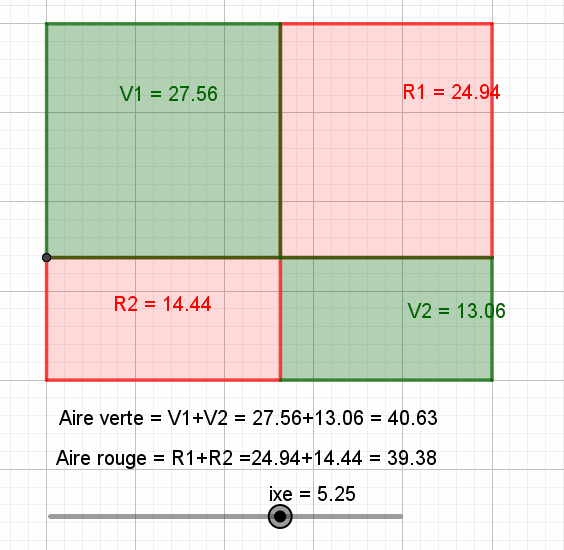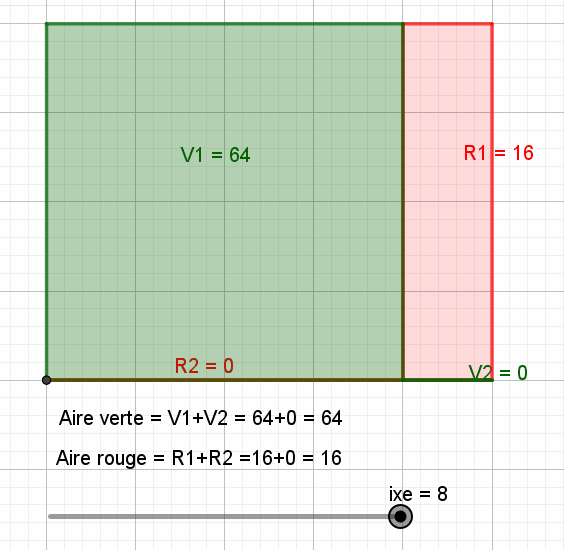
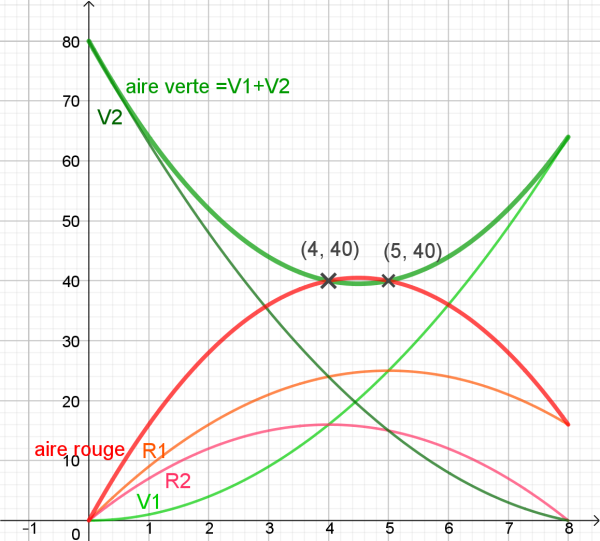
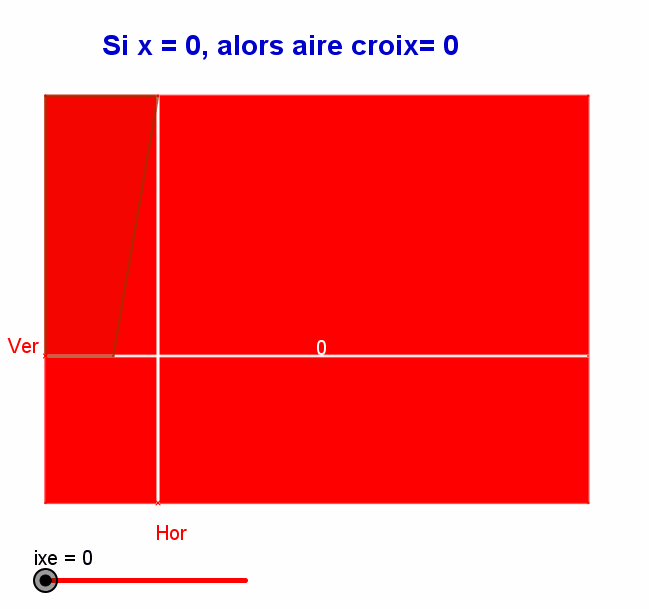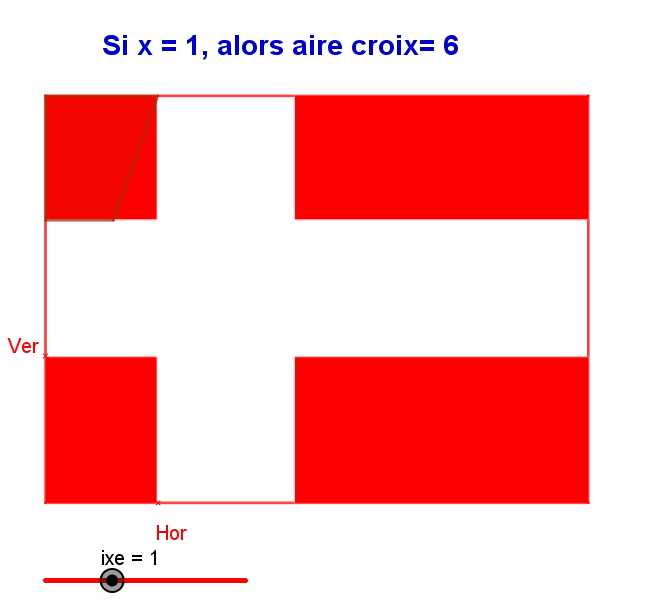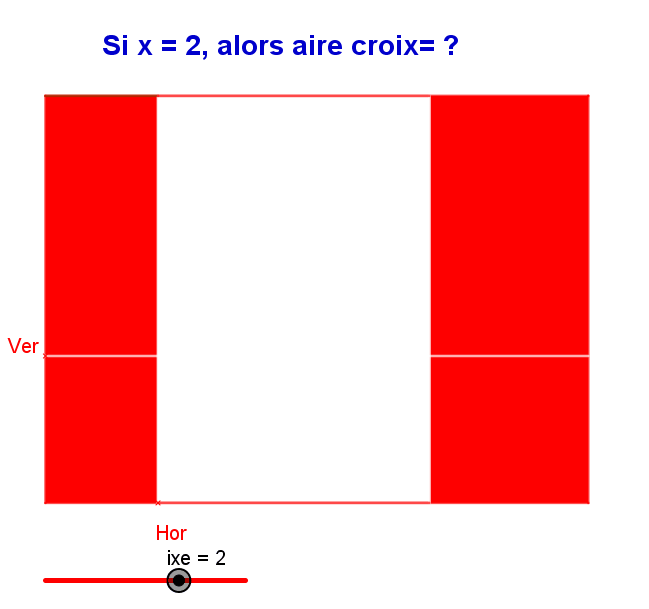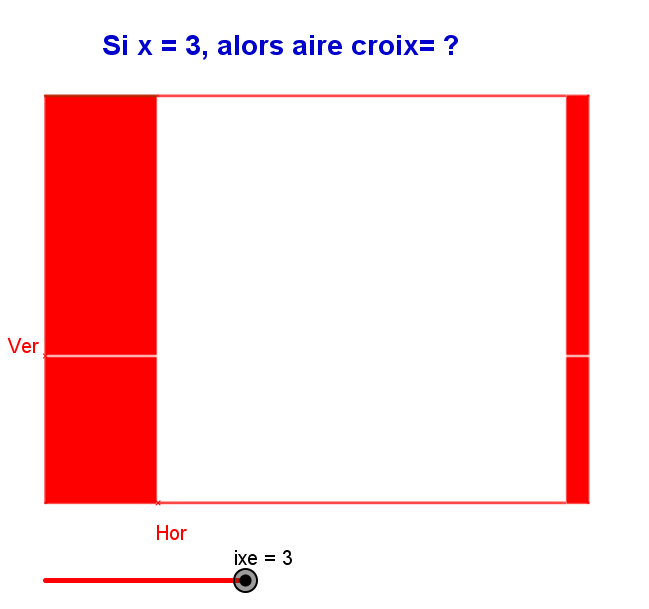
Bonjour, Voici un devoir qui s'adresse à des élèves de Seconde... et quelques digressions graphiques qui en "montrent" les solutions... Pour le plaisir :

Bonjour, donc quelque soit n appartenant à N*, un+1-un ?? 0 => un+1 ?? un => sens de variation de (un)

und Du, Elsa Nicolas, wie geht es dir ? Ich glaube Du bist nicht mehr in "Terminale"...🤭

pour que En appelant x (en m) l'épaisseur de la croix blanche, on a utilisé les données de l'énoncé pour en déduire une équation qui a 2 solutions dont les valeurs sont PEUT-ËTRE les solutions du problème. Pour vérifier, essaye de dessiner (à l'échelle 🤨) un drapeau en prenant comme "épaisseur" de la croix la valeur approchée de ton x2

Cadeau (c'est le jour des cadeaux sur e-bahut jusqu'à ce soir 22h 😄)

mais là il manque des parenthèses dans l'expression des solutions.... et pense à regarder si les 2 solutions de l'équation sont des solutions..... du problème 🤔

D'accord pour le discriminant. C'est bien d'avoir mis des parenthèses autour des nombres négatifs. Il faut utiliser le signe * pour la multiplication afin de ne pas confondre l'inconnue x et le signe multiplié x. A suivre

Oui 🙂. Alors tu résous cette équation du second degré.... Remarque : ax²+bx +c est un polynôme du second degré ax²+bx+c =0 est une équation du second degré

@Mymyyy En plus la réponse écrite sur ce site est fausse et effectivement très incomplète ! j'espère qu'on va faire beaucoup mieux ENSEMBLE sur e-bahut ☺️. Oui. As tu reconnu ce type d'équation ? Si oui donne lui la forme habituelle... comme en cours. PS : tu viens sûrement d'apprendre à résoudre ce type d'équation en classe.

D'accord pour l'aire de la croix blanche. Continue.

Moi cela me plait bien, ce que tu as écrit (mais réduit les termes en x : 4x+3x = ??) Ensuite écrit que cette aire de la croix doit être la moitié de l'aire de ce qui est en rouge donc comme Denis te l'a indiqué, l'aire de la croix est...??? de l'aire totale du drapeau (12 m²). Cette contrainte (condition) permet d'écrire une égalité dans laquelle figure l'inconnue x... donc c'est une équation A RESOUDRE. Essaye et dis nous tes réponses. On va t'aider.

Bonjour, As tu fais un dessin ? c'est primordial. L'aire (avec un "e" c'est mieux 😉) de la partie rouge n'est pas celle du drapeau complet. C'est l'aire du drapeau complet MOINS l'aire de la croix blanche... que l'on ne connait pas. L'épaisseur de la croix blanche est constante mais INCONNUE ; je te conseille de l'appeler x et d'exprimer les aires en FONCTION de cette inconnue x. Montre nous ton dessin et tes tentatives de calcul avec x...