PAVE

L'invasion publicitaire de notre site E-bahut est insupportable... C'est tellement "HENAURME" que l'on peut légitimement se demander s'il ne s'agit pas d'une arnaque. Sans réponse des responsables du site, je rendrai mon tablier de bénévole. Je ne veux pas être impliqué dans cette escroquerie.

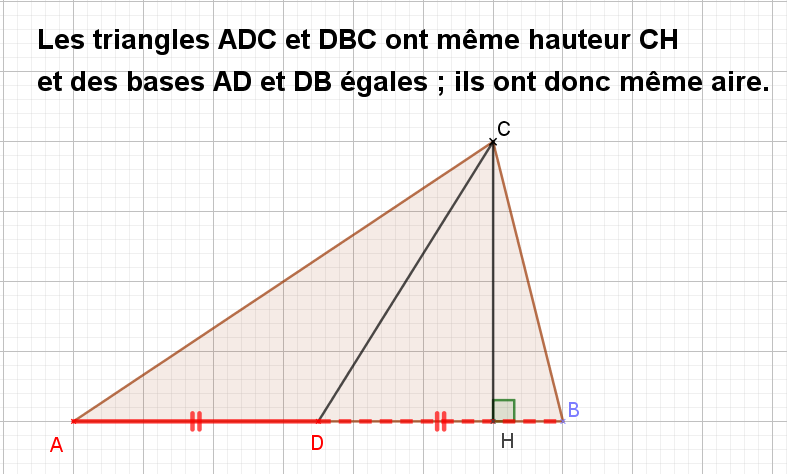
Bonjour les "Pépaires", L'ai-je jamais su ou jamais appris ? ou bien l'ai-je oublié (à nos âges !!) ? Un petit dessin a suffi pour VOIR et me persuader que le "théorème de JulesX" était très facile à démontrer 🧐. Pépaire 77/45 ☺️

Bonjour Jules. Bravo, c'est la bonne réponse Je vais retrouver mon sommeil. Merci ! PAVE

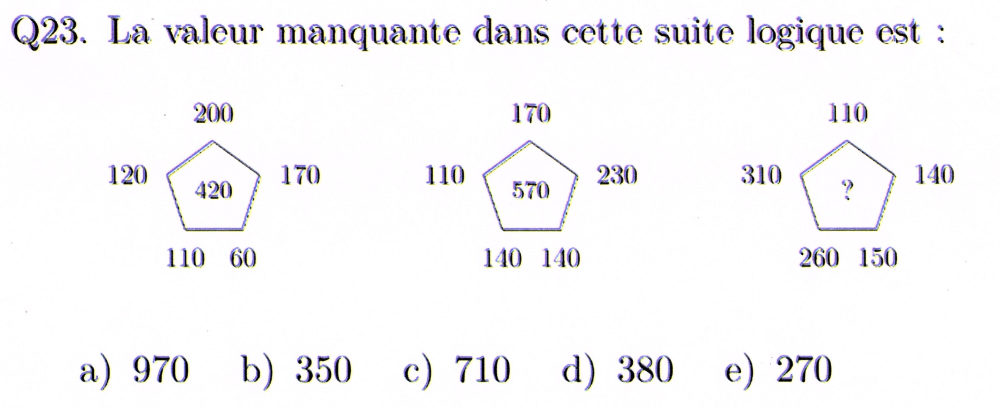
Bonjour Extraite du concours de mathématiques PANGEA 2024 niveau 4ème, cette question Q23 me résiste... 😒 Les 24 autres questions sont sans méchanceté particulière (j'ai trouvé les réponses !!). La logique de celle là m'échappe (et pourtant j'ai connaissance de la bonne réponse !!). D'avance merci de m'ouvrir les yeux !

@ toutes et tous 2016 !! c'est fou comme le temps passe... merci Jules. @ Jogalia As tu essayé de programmer en Python (ou autre langage) l'algorithme demandé ?

Bonjour, 1) Cet énoncé m'a rappelé un problème qui a été (je pense ?) traité sur ce site e-bahut, il y a... quelques années (2019 ??). Je ne suis pas parvenu à retrouver l'énoncé de ce vieux problème (amis collègues, si vous y parvenez... merci) mais dans mes archives, j'ai mis la main sur un fichier GEOGEBRA qui avait été réalisé en ces temps lointains. Jogalia si tu as GEOGEBRA (logiciel interactif gratuit de construction de figures et de courbes) ouvre le fichier joint... La situation représentée a un air de famille avec ton problème !! Qu'en penses-tu ? 2) As tu fait la première question ? Donne nous tes réponses.... on te dira ce que l'on en pense 🧐. 3) Pour la 2ème question, on ne te demande qu'un algorithme.... il te suffit de "décrire" ta démarche. EB20240419 basket.ggb

😊 En répondant à Man_26, j'ai traité une demande de ... 2020 ! Hajime a utilisé ce vieux "post" .

4) Calculer le taux d'évolution soit mais le taux d'évolution DE QUOI ? pas clair !!

2) Le tableau rempli par Hajime (Bonjour !) est exact. 3) C'est le calcul classique d'une moyenne... Moi, je l'ai fait avec un tableur (tu peux essayer 😃) Toi tu as une superbe calculatrice... si tu sais t'en servir, tu vas vite obtenir la bonne réponse. (sinon sors le mode d'emploi ou regarde des tutos et apprends vite à t'en servir 🧐)

Bonjour Man, Tu ne le sais peut-être pas mais nous ne sommes pas des "machines à maths". Alors dire bonjour, cela ne peut pas nuire... pour nous motiver à te répondre 😉 ! 1) c'est élémentaire... Si dans une classe de Seconde, il y a 24 élèves dont 6 filles (les autres sont des garçons !!) alors il y a 6 filles sur 24 élèves la proportion de filles dans cette classe est : 6/24 = 0,25 = 1/4 = 25/100 = 25% Le pourcentage de filles dans la classe est donc 25%. Fais pareil avec tes films (et pense à arrondir... correctement). Si tu veux que l'on vérifie ta réponse... c'est possible (et gratuit 😇)

Merci à vous deux ! Définir l'interception fonctionne sans problème 🙂) Mais Milisandre a disparu... elle n'est même pas venue voir si quelqu'un avait répondu.... 😪

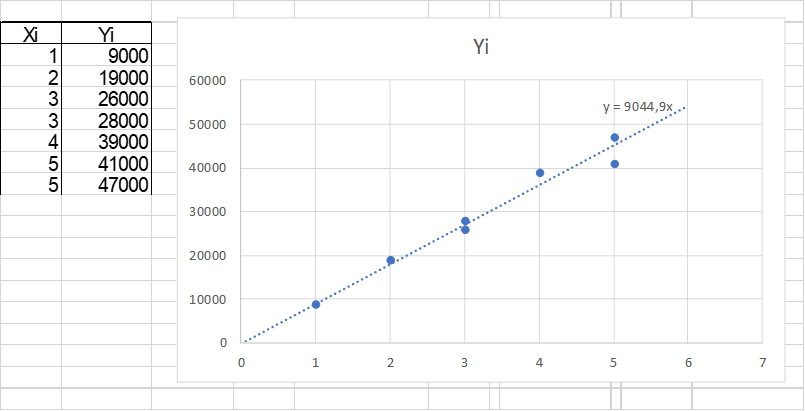
Merci. Je n'ai pas l'équivalent (en direct en tout cas !) sur Excel.

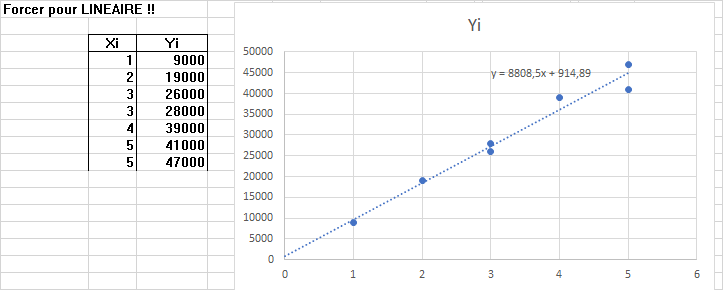
Bonjour Jules, Comment fais tu pour forcer la droite de tendance à passer par l'origine sous Excel ? D'avance merci. Bon dimanche. STP, ne réponds pas en anglais 😄.

Exercices 1 et 3 : ton prof ne vous fait-il pas déterminer les limites à l'infini ? Exercice 2 : P(0) Au rang n= 0, la propriété s'écrit g(0)(x) = (-1)0 (x-0)e-x = 1*x*e-x =xe-x =g(x) = fonction NON dérivée donc P(0) est vraie. Je me suis contenté de mettre en forme ce que tu avais écrit. NB : Pour mieux contrôler, le processus, on peut, je pense, initialiser au rang 1. Si g(x) = xe-x, on calcule sa dérivée première.... et on trouve g'(x) = g(1)(x) =..... moi j'ai trouvé 😇. On vérifie que la propriété au rang 1, donne le même résultat que le calcul ci dessus : P(1) donne g(1)(x) = (-1)1(x-1)e-x = -(x-1)e-x =>la proposition P(n) est donc VRAIE au rang 1 3) HEREDITE Pour montrer que la propriété est vraie pour tout entier n supérieur à 1, on SUPPOSE que la propriété, VRAIE pour n= 1 (et aussi n=2, n=3...), est VRAIE pour une valeur k de n supérieure à 1 : on suppose donc que pour une valeur k de n supérieure à 1, P(k) est VRAIE soit g(k)(x) = (-1)k(x-k)e-x. Il faut alors démontrer que si P(k) est vraie, alors P(k+1) est vraie. Sachant que g(k)(x) = (-1)k(x-k)e-x, on doit dériver g(k)(x) pour obtenir g(k+1)(x). g(k+1)(x) = [g(k)(x)]' = [(-1)k(x-k)e-x]' [NB : l'expression à dériver est de la forme Cuv avec le facteur constant C = (-1)k, le 2ème facteur étant u(x) = (x-k) et le 3ème v(x)=e-x] Je te laisse faire ce calcul (va doucement et écrit bien ☹️) puis conclure.

Exercice 2 : Je ne sais pas si c'est la feuille de ton carnet qui est très étroite ou si c'est que tu écris très gros mais ton brouillon n'est pas très lisible.... En écrivant sur un brouillon de 21 cm de large, ta présentation se trouverait nettement améliorée 😳. Conseil gratuit... Pendant qu'on y est, il faut absolument que tu soignes ta rédaction. En particulier pour ce 2ème exercice... Je suppose que tu as des exemples de raisonnement par récurrence avec une mise en forme très rigoureuse. Il faut absolument suivre le modèle donné par ton prof. 1) Quelle est la PROPRIETE à démontrer ? (elle est donnée par l'énoncé mais il est bon de bien la formaliser et de bien la comprendre) P(n) "pour tout n entier naturel et pour tout x réel, g(n)(x)= (-1)n(x-n)e-x étant entendu que g(n) est la dérivée nième de la fonction g définie par g(x) =xe-x " 2) INITIALISATION 3) HERIDITE 4) Conclusion Essaye de mettre en forme ce que tu as déjà fait et qui montre que tu as compris l'essentiel 😃 As tu COMPRIS l'origine de ton erreur ? la dérivée trouvée est un PRODUIT de 2 facteurs ; le signe du produit se déduit du signe de chacun des facteurs...

Exercice 3 : Si tu avais regardé la COURBE de f, tu aurais su que ta réponse était fausse....

Exercice 1 : il te faut COMPLETER le tableau de variation de f on y faisant figurer les valeurs particulières (maximum et minimum) et aussi les limites à l'infini.

Bonsoir, Pour l'autre exercice, il te faut exploiter les informations données par l'énoncé. A savoir : f(1) = 1/2 Propriété 01 (P01) et surtout cette "bizarrerie" que : f(x+y) = f(x)*f(y) Propriété 02 (P02) [NB : le signe * est celui de la MULTIPLICATION]. 1) Il te faut trouver la valeur de f(2) . Si on écrit 2 sous forme d'une somme x+y : 2= 1+1, alors d'après P02 puis P01, f(2) =.... on aboutit à f(2) = ?? 2) Reste à déterminer f(0). Même procédé ou presque : tu peux écrire que 0+1 = 1. Applique la propriété P02 puis P01.... Je te laisse finir. Pense à calculer la somme finale.

Si tu relis attentivement l'énoncé, la fonction h est involutive si hoh(x)=x Le calcul de hoh(x) qui en découle est un peu délicat mais il se simplifie très vite... et n'oublie pas que tu CONNAIS le résultat à obtenir 😉.

As tu fait l'exercice 3 ? f est de la forme eu donc f ' est de la forme.... Cela c'est du cours que tu dois savoir. L'étude de la fonction f ne pose pas de problème ; c'est de l'ultra classique 1) domaine de déf ? avec une exponentielle... 2) calcul de la fonction dérivée 3) étude du signe de la dérivée puis tableau de variation de f 4) penser à vérifier en jetant un œil sur la courbe de f Essaye et montre ce que tu obtiens ; on te dira si c'est bon mais surtout, s'il y a un problème dans tes réponses, on te dira comment faire...pour ne plus refaire cette erreur 🤥

Par contre tu as dû voir en cours la notion de fonction composée....et cela suffit pour traiter cet exercice 🙂 !! Dans mon message, je t'ai rappelé la définition de h= gof (cela tu dois connaitre) et en application j'ai proposé le cas particulier où g est égal à f => h=fof soit h(x) = f[f(x)] Prends la fonction f donnée dans ton exercice et calcule f[f(x)]. Essaye....

Quelques rappels :

Cela me fait plaisir de te voir réapparaitre sur ce fil. C'est bien de persévérer. On va t'aider d'autant plus que les réponses que tu as données sont bonnes comme te l'a dit Jules (merci à lui d'avoir pris le relai... et bonne année à vous deux☺️). Dans l'étude d'une fonction f, 1. on calcule la fonction dérivée f ' . Tu as obtenu ici f '(x) = 3x²+6x-45 qui est un polynôme du second degré (si besoin revoir le cours de 1ère 😟) 2. on étudie le SIGNE de f '(x) la dérivée : en première tu as appris à étudier le SIGNE d'un trinôme du second degré ax²+bx+c (à revoir si besoin) On présente le résultat sous forme d'un tableau.... donnant le SIGNE de la dérivée. valeurs de x |.................. Signe de f '(x)|......................... 3. le SIGNE de la dérivée f ' donne le SENS DE VARIATION de la fonction f. On présente le résultat sous forme d'un tableau de VARIATION. On peut simplement ajouter une ligne au tableau de Signes précédent. valeurs de x |.................. Signe de f '(x)|......................... SENS de variation de f | 4. on vérifie que le tableau obtenu est cohérent (compatible) avec la courbe représentative de f (avec un peu d'expérience, 2 minutes suffisent pour obtenir cette courbe sur ta calculatrice... VERIFIER est fondamental !!)

Bonjour, Il y a bien longtemps que je n'avais trouvé cette notion (l'involution) dans un exercice de lycée. ll serait intéressant de savoir comment cette notion est abordée en Terminale.