-
Compteur de contenus
13 394 -
Inscription
-
Dernière visite
-
Jours gagnés
453
Type de contenu
Profils
Forums
Blogs
Galerie
Boutique
Tout ce qui a été posté par Barbidoux
-
SalutDenis
Dans ta réponse
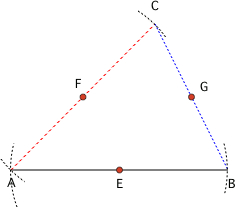
3) Quand la balle touche le sol, sa hauteur, donc h(x) est nulle. Résous h(x) = 0. Est-ce que c'est avant C ?
Je ne crois pas qu'elle soit capable de résoudre cette équation à son niveau (3èm). Le plus simple selon moi serrait pour elle de calculer l'image de 18 par h et d'en tirer les conclusions qui s'imposent.
Je te souhaite une bonne soirée
Amitiés
Bernard Le Gorrec