Barbidoux

1————————— H3SbCl6+NaNO2 —————— H3SbCl6=Sb^(5+)+6*Cl^(-)+3*H^(+)+2*^(e) 2*H^(+)+NO2^(-)+e^(-)=NO+H2O ——————— H3SbCl6+4*H^(+)+2*NO2^(-)=Sb^(5+)+6*Cl^(-)+3*H^(+)+2*NO+2*H2O H3SbCl6+H^(+)+2*NO2^(-)=Sb^(5+)+6*Cl^(-)+2*NO+2*H2O 2————————— Electrode de verre cf. P209 du document que je t’ai envoyé 3————————— PH-mètre simple millivolt mètre à très forte impédance d’entrée (>1 GΩ) 4————————— la tension de l’électrode variant linéairement avec le logarithme de la concentration de l’espèce X est sélective de cette espèce. 6————————— Qu’elles son t les réactions à l’anode et la cathode ? ———— Le régime de fonctionnement du générateur n’étant pas défini impossible de répondre. Ses pôles sont invariant, mais cathode et anode changent selon que l’on décharge ou charge le générateur Je te joins un exercice corrigé concernant cet accumulateur et son fonctionnement. AccuPb.pdf

un peu d'aide :

………NH4HS(s)=…..NH3(g)….+….H2S(g) teq……..excès………..….x……….......…x Kp={PNH3}*P{H2S} {PNH3}=P{H2S}=√Kp=0.33 atm a————— ………NH4HS(s)=…..NH3(g)….+….H2S(g) teq……..excès……….x+0.5………..…x b)——————— x est solution de l’équation 0.11=(x+0.5)*x ==> x=0.165

un peu d'aide ....

un peu d'aide.....

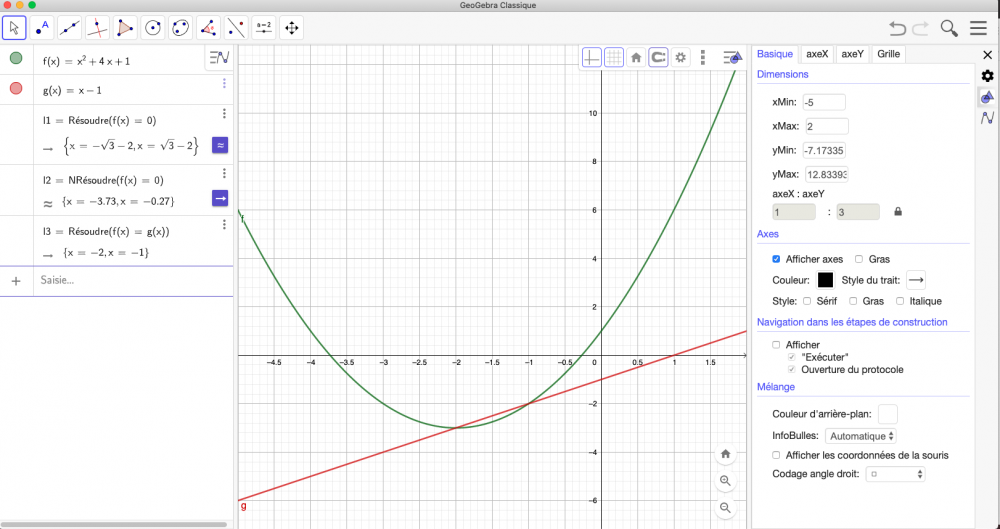
Pas sur Geogebra 6 version Mac. Si l'on désire un graphe orthonormé (on fixe le rapport des unités à 1) les modifications de l'intervalle en x et y sont liées et il est impossible de les régler de manière indépendantes. Si on fixe les intervalles en x et y alors le rapport des unités en x et y ne peut être imposé.

Les versions de "Geogebra" sont nombreuses sur une même plateforme (sur Mac par exemple Geogebra 5, Classique 6, GeoGebra Graphing Calculator etc...) et on ne peut pas toujours faire ce que l'on veut en matière de fenêtre dans lequel se trace un graphe. L'instruction Si(-5<x<2,x²+4x+1) équivalente à f(x) =x²+4x+1 , (-5<x<2) limite le tracé du graphe dans l'intervalle [-5,2] mais ne garanti pas que l'axe des x apparait dans cet intervalle. Sur la version Classique 6 en ma possession pour jouer sur l'intervalle de tracé on peut utiliser la fonction basique et régler l'intervalle en x. L'amplitude en y est modifiée en jouant sur le rapport des unités sur les échelles en x et y. Le problème c'est qu'aucun tutoriel ou manuel des différentes versions de Geogebra semble exister (du moins je n'en ai pas trouvé) et l'utilisation de ce logiciel par ailleurs assez génial est parfois assez rebutante....

celles qui ont même coefficient directeur d1:y=4; y=-28 (coef directeur =0) et d4:y=2x+3 ; ; d6:y=2x (coef directeur =2)

Il suffit de lire sur le diagramme E-pH qui indique que l'hydroxyde de cadmium précipite à pH=8.1 donc pour une concentration en OH- égale à 1014-8.1=10-5.9 mol/L lorsque la concentration en ion Cd2+ est égale à 10-2 (valeur des concentration en espèces dissoutes Cd2+ ou HCd02- pour laquelle il a été tracé)

Qu'elle concentration en OH- ?

Tu as bine fait de poser la question car j'avais zappé que le diagramme E-pH donné avait été tracé pour {Cd2+}=10-2 . Par convention les valeurs E° des couples redox sont donnés par rapport à l'électrode standard à hydrogène ESH, ou NHE ce qui correspond à une valeur de pH égale à 0. La valeur E° (Cd2+/Cd) ne variant pas avec la valeur du pH c'est donc une droite parallèle à l'axe des pH sur le diagramme E-pH qui coupe l'axe des tension au point E=E°(Cd2+/Cd)+(0.06/2) lg{{Cd2+} ==>à 25° C alors E°(Cd2+/Cd)=E-0.3*lg10-2=-0.46+0.06=-0.40 V/ENH

23X07=23000+X07 1000 est divisible par 4 et 8 mais X07 ne l'est pas car tout nombre divisible par 4 ou 8 est pair or X07 ne l'est pas quelques soit X appartenant à {0,1.......,9} règle de divisibilité par 3 = somme des chiffres est un multiple de 3. Il faut donc que 2+3+X+7 =0 [3] donc X =0[3] . En conséquence X={0,3,6,9} règle de divisibilité par 9=somme des chiffres est un multiple de 9 donc il faut que 2+3+X+7 =0[9] donc que X+3=0[9]. En conséquence X={6}

23X07 = 2*104+3*103+X*102+0*101+7*100=20000+3000+X*100+0*10+7

un nombre entier de n chiffres dans une base décimale s'exprime selon an-1*10n-1+an-2*10n-2+.........+a0*100 avec {an-1, an-2,......... a0} entiers appartenant à l'intervalle [0,9]

23X07=23000+X07 pas divisible par 4 ni par 8 quelque soit X et critères de divisibilité par 3 ou par 9 pour la division par 3 et par 9. Exemple par 3 ==> X={0,3,6,9}

23X2=2300+X2 pour que ce nombre soit divisible par 4 il faut et il suffit que X2 le soit ce qui donne X={1,3,5,7,9}

pour 4 on a N=23X2=23*100+X2 tu sais que 100 est divisible par 4 il vaut donc que X2 le soit , pareil et pour 8 et pour 3 et 9 utilises les critères de divisibilités par ces chiffres

Je te montre pour le premier .... 27=3*9 ==> 272=9*81=729 et 27=(30-3) ==> 27^2=(30-3)2=900-180+9=729.... à toi pour la suite